8 класс. Урок № 10. Решение задач по теме: "Тепловой баланс".

Рассмотрим алгоритм решения задач на тепловой баланс:

1. Понять предложенную задачу (увидеть физическую модель).
2. Анализ (построить математическую модель явления):
1. Определить изолированную систему.
2. Установить у каких тел внутренняя энергия уменьшается, а у каких – возрастает.
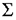
3. Составить уравнение теплового баланса (U = 0), при записи которого в выражении cm(t2 – t1), для изменения внутренней энергии, нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака.
3. Полученное уравнение решить относительно искомой величины.
4. Решение проверить и оценить критически.

Пример решения задачи:

Задача1. 

Сколько кипятка нужно долить в сосуд, содержащий 2 кг воды при температуре 350С, чтобы температура в сосуде увеличилась до 650С? 

Пояснения учителя: в основе решения данной задачи лежит закон сохранения внутренней энергии: для любой изолированной системы при любых изменениях внутри неё внутренняя энергия остаётся неизменной. Как можно применить этот закон для решения задачи? Если привести в соприкосновение два тела разной температуры ( в нашем случае, это вода при температуре 350С и кипяток ( вода при 1000С), то, во-первых, теплообмен будет протекать до тех пор, пока температуры тел не сравняются (в задаче температура станет равной 650С), и, во-вторых, первое тело будет передавать тепла ровно столько(Qотд), сколько второе тело получит(Qпол). 

Таким образом, из закона сохранения тепловой энергии имеем: Qотд = Qпол. Это соотношение называют уравнением теплового баланса.
А теперь запишем краткое условие, введя удобные и понятные обозначения:
mх - масса «холодной воды» (воды, взятой при 350С),
mг - масса «горячей» (кипятка при 1000С),
tх – начальная температура «холодной воды»,
tг – начальная температура «горячей воды»,
tсм – температура смеси.

Дано: Решение.

При решении задачи используем
mх = 2кг формулу:Q=Сm(t2 - t1), где Q – коли-
tх = 350С чество теплоты, полученное при нагрева-
tг = 1000С нии тела( отданное при охлаждении),
tсм = 650С m – масса вещества, t2 – конечная темпера-
С= 4200 Дж/(кг 0С) тура, t1 – начальная температура.
Но в случае данной задачи, начальная
температура «холодной воды» tх, началь-mг - ? ная температура кипятка tг. 

Итак, запишем уравнение теплового
баланса:
Qотд = Qпол
Qотд = -С mг(tсм - tг) (*),
Qпол = С mх(tсм - tх) (**).
Знак «минус» в формуле для Qотд означает, что теплоту при остывании кипяток отдаёт.
Приравнивая правые части уравнений (*) и (**), имеем: -С mг(tсм - tг)= С mх(tсм - tх). 

Внимание! Объяснение перестановки слагаемых tсм и tг в скобках. 

Из курса алгебры известно: знак «минус» перед скобками можно опустить, поменяв местами слагаемые в скобках( заметим, что одновременно можно обе части уравнения поделить на значение С, отличное от нуля). В результате получаем уравнение:
mг(tг - tсм) = mх(tсм - tх ).
Выражаем из уравнения искомую величину mг и имеем расчётную формулу:
mг= mх(tсм - tх )/(tг - tсм)
После подстановки данных и необходимых вычислений, получаем значение массы кипятка mг=1,7кг.
Ответ: mг=1,7кг.
Данная методика позволяет решать и более сложные задачи «на тепловой баланс».

Задача2.

В 200г воды при 200С помещают 300г железа при 100С и 400г меди при 250С. Найти установившуюся температуру.

Дано: СИ Решение.

m в=200 г 0,2 кг Составим уравнение теплового
m ж=300 г 0,3 кг баланса:
m м=400 0,4 кг Q1 + Q2= Q3 (1), где
t в=200С Q1-количество теплоты,
t ж=100С полученное водой;
t м =250С Q2- количество теплоты,
С в= 4200 Дж/(кг 0С) полученное железом;
С ж=460 Дж/(кг 0С) Q3-количество теплоты,
С м= 400 Дж/(кг 0С) отданное медью.

t см - ?

Q1= С в m в (t см - t в)
Q2= С ж m ж (t см - t ж)
Q3= -С м m м (t см - t м)
Подставляем правые части равенств в уравнение (1),не забываем поменять местами слагаемые в скобках последнего равенства, опустив «минус».
С в m в (t см - t в) + С ж m ж (t см - t ж) = С м m м (t м - t см). Произведя алгебраические преобразования по раскрытию скобок, приведению подобных слагаемых, выражению искомой величины, имеем расчётную формулу для нахождения температуры смеси:
t см= (С в m в t в + С ж m ж t ж + С м m м t м)/ (С в m в + С ж m ж + С м m м ).
Выполняем необходимые вычисления и находим значение искомой величины: t см =190С.
Ответ: t см =190С.

Итак, можно выделить следующий алгоритм решения задач на «тепловой баланс»:

• по данным задачи составить общее уравнение теплового баланса;
• записать соответствующие равенства для каждой из величин теплоты, входящих в общее уравнение теплового баланса;
• подставить правые части записанных равенств в уравнение теплового баланса;
• поменять местами слагаемые в скобках, перед которыми стоит знак «минус»;
• выразить искомую величину из полученного уравнения.