Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения, или, говорят, меняется проекция вектора скорости.
Неравномерное движение бывает двух видов — ускоренным, это когда скорость тела увеличивается с течением времени, и замедленным, когда скорость тела уменьшается с течением времени.Прямолинейным равноускоренным движением называется такое движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.
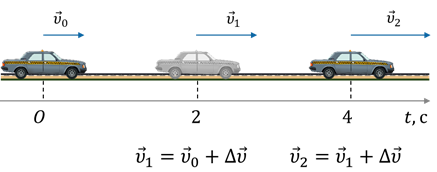
Величина, характеризующая быстроту изменения скорости тела при равноускоренном движении называется ускорением и обозначается малой латинской буквой а.
Для того, чтобы найти ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло. Таким образом, равноускоренное движение — это движение с постоянным ускорением.
Неравномерное движение бывает двух видов — ускоренным, это когда скорость тела увеличивается с течением времени, и замедленным, когда скорость тела уменьшается с течением времени.Прямолинейным равноускоренным движением называется такое движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.


Для того, чтобы найти ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло. Таким образом, равноускоренное движение — это движение с постоянным ускорением.
За единицу ускорения в СИ принимается ускорение такого прямолинейного равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с:
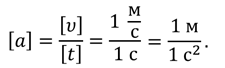 Ускорение — это векторная величина, направление которой, как следует из формулы, совпадает с направлением вектора изменения скорости тела.Например, при разбеге самолёта направление вектора ускорения и векторов скорости совпадают и самолёт движется ускоренно. При посадке, наоборот, самолёт замедляет своё движение. В этом случае вектор ускорение и векторы скорости имеют противоположные направления. Поэтому самолёт движется замедленно.
Ускорение — это векторная величина, направление которой, как следует из формулы, совпадает с направлением вектора изменения скорости тела.Например, при разбеге самолёта направление вектора ускорения и векторов скорости совпадают и самолёт движется ускоренно. При посадке, наоборот, самолёт замедляет своё движение. В этом случае вектор ускорение и векторы скорости имеют противоположные направления. Поэтому самолёт движется замедленно.

Конечно же, как и в случае со скоростью, при решении большинства задач, мы будем пользоваться формулой, в которую входит не сам вектор ускорения, а его проекция на координатную ось.
 Для того, чтобы найти ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло. Таким образом, равноускоренное движение — это движение с постоянным ускорением.
Для того, чтобы найти ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло. Таким образом, равноускоренное движение — это движение с постоянным ускорением.
За единицу ускорения в СИ принимается ускорение такого прямолинейного равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с:
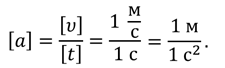 Ускорение — это векторная величина, направление которой, как следует из формулы, совпадает с направлением вектора изменения скорости тела.
Ускорение — это векторная величина, направление которой, как следует из формулы, совпадает с направлением вектора изменения скорости тела.

За единицу ускорения в СИ принимается ускорение такого прямолинейного равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с:

Например, при разбеге самолёта направление вектора ускорения и векторов скорости совпадают и самолёт движется ускоренно. При посадке, наоборот, самолёт замедляет своё движение. В этом случае вектор ускорение и векторы скорости имеют противоположные направления. Поэтому самолёт движется замедленно.
Конечно же, как и в случае со скоростью, при решении большинства задач, мы будем пользоваться формулой, в которую входит не сам вектор ускорения, а его проекция на координатную ось.
 Основная задача кинематики состоит в том, чтобы найти положение тела в любой момент времени. Для того, чтобы ее решить, нужно сначала суметь найти скорость тела в любой момент времени. Для этого следует знать закон, по которому происходит изменение мгновенной скорости от времени для равноускоренного движения. Здесь все просто, достаточно выразить вектор скорости из формулы определения ускорения тела, воспользовавшись известными математическими приемами.
Основная задача кинематики состоит в том, чтобы найти положение тела в любой момент времени. Для того, чтобы ее решить, нужно сначала суметь найти скорость тела в любой момент времени. Для этого следует знать закон, по которому происходит изменение мгновенной скорости от времени для равноускоренного движения. Здесь все просто, достаточно выразить вектор скорости из формулы определения ускорения тела, воспользовавшись известными математическими приемами.
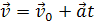 Полученное уравнение называется уравнением скорости для равноускоренного движения. Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя, поэтому перепишем уравнение в проекции на ось х.
Полученное уравнение называется уравнением скорости для равноускоренного движения. Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя, поэтому перепишем уравнение в проекции на ось х.
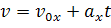 Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.
Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.



Как и в случае равномерного прямолинейного движения тела, зависимости кинематических величин от времени при равноускоренном движении можно изобразить графически. Для начала нарисуем графики зависимости ускорений для трех тел от времени.

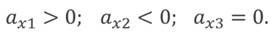
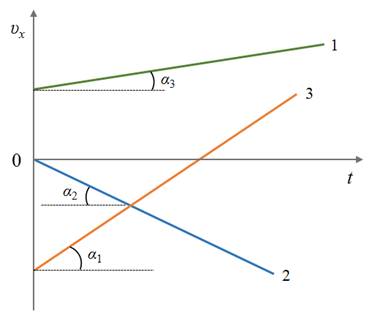 На графике прямая 1 соответствует движению с положительным ускорением и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением без начальной скорости, а прямая 3 — движению тела с положительным ускорением и отрицательной начальной скоростью.
На графике прямая 1 соответствует движению с положительным ускорением и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением без начальной скорости, а прямая 3 — движению тела с положительным ускорением и отрицательной начальной скоростью.

Так как в случае равноускоренного движения модуль и направление вектора ускорения не меняется, то график ускорения имеет вид прямой, параллельной оси времени.
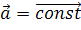

При этом график располагается над осью времени, если тело движется равноускорено; под осью времени — в случае равнозамедленного движения (то есть когда проекция ускорения на координатную ось меньше нуля); и будет совпадать с осью времени, если тело движется прямолинейно и равномерно.
Теперь изобразим графики зависимости скорости от времени. Известно, что при равноускоренном движении скорость с течением времени не остается постоянной, а меняется со временем. При этом, как видно из уравнения, зависимость скорости от времени является линейной функцией и поэтому график скорости имеет вид прямой, наклоненной к оси времени. Причем, чем больше угол наклона, тем большее ускорение имеет тело.

Рассмотрим подробнее график скорости для тела 3. Что можно сказать про эту точку? Какие изменения происходят с движением тела в ней? В этой точке скорость тела меняет свое направление на противоположное. Такая точка называется точкой поворота.




Комментариев нет:
Отправить комментарий