Формулировка закона всемирного тяготения такова: сила взаимного притяжения двух тел прямо пропорциональна произведению их масс и обратно пропорционально квадрату расстояния между ними.

Впервые гравитационная постоянная была измерена Генри Кавендишем в 1798 году. С помощью крутильных весов, ему удалось определить значение гравитационной постоянной достаточно точно (оно почти совпадает с принятым сегодня значением).
 Крутильные весы представляют собой следующую установку: на тонкой упругой нити подвешено лёгкое коромысло с двумя шарами на концах. Рядом закреплены два значительно более тяжёлых шара (в эксперименте Кавендиша легкие шары имели массу 775 г, а тяжёлые – 49,5 кг). В результате гравитационного взаимодействия, коромысло поворачивалось и закручивало нить. Зная упругие свойства нити, Кавендишу удалось измерить силу притяжения. Поскольку, массы шаров ему были известны, так же, как и расстояние между ними, Кавендиш смог вычислить гравитационную постоянную.
Крутильные весы представляют собой следующую установку: на тонкой упругой нити подвешено лёгкое коромысло с двумя шарами на концах. Рядом закреплены два значительно более тяжёлых шара (в эксперименте Кавендиша легкие шары имели массу 775 г, а тяжёлые – 49,5 кг). В результате гравитационного взаимодействия, коромысло поворачивалось и закручивало нить. Зная упругие свойства нити, Кавендишу удалось измерить силу притяжения. Поскольку, массы шаров ему были известны, так же, как и расстояние между ними, Кавендиш смог вычислить гравитационную постоянную.
 Несмотря на это, все тела находятся в состоянии покоя. Дело в том, что опора, по третьему закону Ньютона, действует, например, на горшок, с той же силой, что и горшок давит на неё. Эта сила называется реакцией опоры. Итак, мы выяснили что, исходя из третьего закона Ньютона, реакция опоры равна по модулю весу тела. Поскольку тело покоится, равнодействующая сила равна нулю. Следовательно, реакция опоры должна уравновешивать силу тяжести (в противном случае, тело бы падало по направлению к центру Земли).
Несмотря на это, все тела находятся в состоянии покоя. Дело в том, что опора, по третьему закону Ньютона, действует, например, на горшок, с той же силой, что и горшок давит на неё. Эта сила называется реакцией опоры. Итак, мы выяснили что, исходя из третьего закона Ньютона, реакция опоры равна по модулю весу тела. Поскольку тело покоится, равнодействующая сила равна нулю. Следовательно, реакция опоры должна уравновешивать силу тяжести (в противном случае, тело бы падало по направлению к центру Земли).

Необходимо отметить, что если тела не являются материальными точками, то за расстояние между ними принимается расстояние между центрами тяжести этих тел. В формуле мы видим коэффициент пропорциональности, который называется гравитационной постоянной. Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массами 1 кг, если расстояние между ними составляет 1 метр.
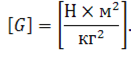

Видеоурок: Гравитационное взаимодействие. Закон всемирного тяготения.
Видеурок: Сила тяжести. Вес тела
Интерактивный тест по материалам урока
Гравитационная постоянная является очень важной константой, поскольку именно с её помощью люди смогли вычислить массу Земли, Луны, Солнца и так далее. Но как вычислить саму гравитационную постоянную?Видеурок: Сила тяжести. Вес тела
Интерактивный тест по материалам урока
Впервые гравитационная постоянная была измерена Генри Кавендишем в 1798 году. С помощью крутильных весов, ему удалось определить значение гравитационной постоянной достаточно точно (оно почти совпадает с принятым сегодня значением).

Необходимо отметить, что закон всемирного тяготения дает точный результат, в трех случаях:
1) Если оба тела имеют форму шара и являются однородными.
2) Если размеры тел ничтожно малы, по сравнению с расстоянием между ними.
3) Если одно из тел обладает формой шара и его размеры многократно больше размеров второго тела любой формы.
1) Если оба тела имеют форму шара и являются однородными.
2) Если размеры тел ничтожно малы, по сравнению с расстоянием между ними.
3) Если одно из тел обладает формой шара и его размеры многократно больше размеров второго тела любой формы.
Примеры решения задач.
 Задача 2. Вычислите, на какой высоте над поверхностью Земли должен находиться геостационарный спутник.
Задача 2. Вычислите, на какой высоте над поверхностью Земли должен находиться геостационарный спутник.
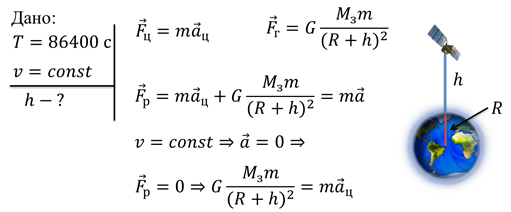 Необходимо отметить, что в задачах мы принимали орбиты планет за окружности для упрощения расчетов. В действительности, планеты Солнечной системы двигаются по эллиптическим орбитам, поэтому, когда мы говорим о расстоянии от планеты до Солнца, мы имеем ввиду средний радиус её орбиты.
Необходимо отметить, что в задачах мы принимали орбиты планет за окружности для упрощения расчетов. В действительности, планеты Солнечной системы двигаются по эллиптическим орбитам, поэтому, когда мы говорим о расстоянии от планеты до Солнца, мы имеем ввиду средний радиус её орбиты.
Задача 1. Юпитер обладает массой
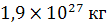 и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.
и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.
Поскольку закон всемирного тяготения является одним из универсальных законов природы, он одинаково выполняется для всех тел, имеющих массу. Рассмотрим произвольное тело (масса и размеры которого ничтожно малы по сравнению с массой и размерами Юпитера).
 и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.
и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.Поскольку закон всемирного тяготения является одним из универсальных законов природы, он одинаково выполняется для всех тел, имеющих массу. Рассмотрим произвольное тело (масса и размеры которого ничтожно малы по сравнению с массой и размерами Юпитера).

На первый взгляд может показаться, что в задаче нет исходных данных. Но если мы внимательно рассмотрим ситуацию, то убедимся, что некоторые данные у нас есть. В первую очередь, — это период обращения спутника: разумеется, он должен быть равен периоду обращения Земли вокруг своей оси. И самое главное: спутник должен двигаться с постоянной скоростью, поскольку Земля тоже двигается с постоянной скоростью.

силы тяжести — это сила, с которой Земля притягивает тело, находящееся на её поверхности (или вблизи этой поверхности). Именно под действием силы тяжести, тела могут находиться в свободном падении. Находясь в свободном падении можно ясно ощутить состояние невесомости, то есть, отсутствие веса. Рассмотрим эти явления более подробно.
Вес тела — это сила, с которой тело действует на горизонтальную опору или растягивает подвес. Надо сказать, что вес — это частный случай силы упругости. Рассмотрим простой пример. В помещении вы видите сидящего человека, горшки с растениями, часы, висящие на стене и так далее. На все эти тела, несомненно, действует сила тяжести.
Таким образом, если тело покоится на горизонтальной поверхности, или двигается равномерно и прямолинейно, то вес тела равен силе тяжести.
А теперь, давайте рассмотрим, что произойдет, если опора будет двигаться с ускорением. Классический пример подобной ситуации — это движение лифта. При начальном движении лифта вверх, ускорение, конечно, направлено вверх.
 Применим второй закон Ньютона:
Применим второй закон Ньютона:
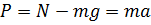
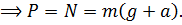 Из этого уравнения, мы видим, что вес тела увеличивается при ускоренном движении опоры вверх. Это явление называется перегрузкой. Действительно, при рывке лифта вверх, мы чувствуем некое давление.
Из этого уравнения, мы видим, что вес тела увеличивается при ускоренном движении опоры вверх. Это явление называется перегрузкой. Действительно, при рывке лифта вверх, мы чувствуем некое давление.



Нетрудно догадаться, что при ускоренном движении вниз, происходит противоположное явление: вес тела уменьшается.
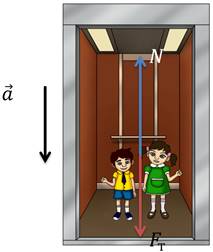 В этом можно убедиться, если вновь применить второй закон Ньютона:
В этом можно убедиться, если вновь применить второй закон Ньютона:
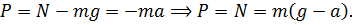


Как видно, из уравнения, при движении вниз с ускорением свободного падения, вес тела обратится в ноль:
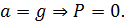
Это явление называется невесомостью. И правда, при рывке лифта вниз, мы ощущаем некую легкость.
Так, космонавты, находящиеся на космической станции, испытывают состояние невесомости. Они, фактически находятся в свободном падении, но падают, как бы, вокруг Земли. Дело, конечно, в их орбитальной скорости, достаточной для того, чтобы находиться на околоземной орбите.
 При этом, стакан не будет оказывать никакого воздействия на поднос, то есть не будет обладать весом. Точно также, мотоциклист, едущий с постоянной скоростью, будет действовать на сиденье мотоцикла силой тяжести. Но после прыжка на трамплине, и мотоциклист, и мотоцикл будут находиться в свободном падении.
При этом, стакан не будет оказывать никакого воздействия на поднос, то есть не будет обладать весом. Точно также, мотоциклист, едущий с постоянной скоростью, будет действовать на сиденье мотоцикла силой тяжести. Но после прыжка на трамплине, и мотоциклист, и мотоцикл будут находиться в свободном падении.


Приведем пару примеров. Допустим, вы поставите стакан с водой на поднос. Очевидно, что стакан будет действовать на поднос с силой: Fт = mg. Но, как вы знаете, если вы отпустите поднос, то и стакан, и поднос будут находиться в свободном падении.


Таким образом, вес мотоциклиста будет равен нулю, до тех пор, пока он не приземлится.
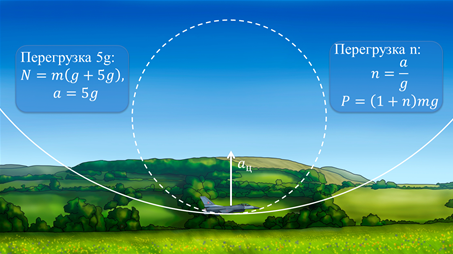
Примером перегрузки может быть выход пилота из пике.

В нижней точке, его центростремительное ускорение будет направлено вверх, что приведет увеличению веса пилота. Пилоты истребителей испытывают перегрузки до 30g. Перегрузки часто измеряются в единицах измерения g. То есть, например, перегрузка 5g означает, что вес пилота увеличился в 6 раз (в состоянии покоя наша перегрузка равна g). Иногда перегрузку обозначают буквой n, и она является безразмерной величиной, равной отношению ускорения движения к ускорению свободного падения.Примером перегрузки может быть выход пилота из пике.


Таким образом, вес тела при перегрузках можно вычислить по формуле:
 Для примера вычислим перегрузку, которую испытывает пилот в нижней точке пике в вертикальной плоскости, если радиус кривизны траектории полёта равен 400 м, а скорость самолёта равна 1080 км/ч.
Для примера вычислим перегрузку, которую испытывает пилот в нижней точке пике в вертикальной плоскости, если радиус кривизны траектории полёта равен 400 м, а скорость самолёта равна 1080 км/ч.
 Для примера вычислим перегрузку, которую испытывает пилот в нижней точке пике в вертикальной плоскости, если радиус кривизны траектории полёта равен 400 м, а скорость самолёта равна 1080 км/ч.
Для примера вычислим перегрузку, которую испытывает пилот в нижней точке пике в вертикальной плоскости, если радиус кривизны траектории полёта равен 400 м, а скорость самолёта равна 1080 км/ч.





Комментариев нет:
Отправить комментарий