9 класс. Урок 70-71. Закон всемирного тяготения. Сила тяжести. Ускорение свободного падения.

Впервые Ньютон доказал, что причина, вызывающая падение яблока на землю, вращение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения, действующая между любыми телами во Вселенной

Имя Исаака Ньютона прочно связано с открытием «Закона всемирного тяготения». На самом деле великое открытие учёного — это последнее звено в цепи предыдущих и более частных открытий.

Видеоурок: Закон всемирного тяготения

Видеоурок: Ускорение свободного падения

Интерактивный тест: Закон всемирного притяжения

История открытия закона всемирного тяготения начинается с вхождения в науку системы Коперника. Только после установления гелиоцентрической системы мира оказалась возможной постановка задачи раскрытия механизма солнечной системы.

Первая мысль принадлежала английскому ученому Гильберту. Он предположил, что планеты солнечной системы представляют собой гигантские магниты, поэтому силы, связывающие их, имеют магнитную природу. Мысль эта была следствием установления Гильбертом факта эквивалентности силового поля намагниченного шара и Земли.

Первыми количественными законами, открывшими путь к идее всемирного тяготения, были законы Иоганна Кеплера.

В 1609 г. Кеплер опубликовал два эмпирических закона движения планет, открытые им при обработке данных, относящихся к Марсу. А в 1618 г. Кеплер находит третий закон, связывающий движения различных планет вокруг Солнца.

После появления этих законов оказалась возможной строгая постановка механической задачи на определение движения планет.

Наряду с работами Кеплера результаты, достигнутые Галилеем при изучении законов падения тел, подготовляли Ньютону почву в другом направлении. Галилей был основателем рациональной динамики, т. е. учения о движении тел под действием сил. Галилей сумел отделить в реальном движении случайные силы (трение, сопротивление воздуха и т. д.) и при изучении движения тел по наклонной плоскости пришел к заключению, что без действий сил тело будет двигаться равномерно или же останется в покое.

Первый эскиз решения механической задачи на определение движения планет дал Роберт Гук. В 1674 г. он опубликовал большой мемуар «Попытка доказательства годичного движения на основе наблюдений». В нем он писал: «Я изложу систему мира, во многих частностях отличающуюся от всех до сих пор известных систем, но во всех отношениях согласную с обычными механическими законами. Она связана с тремя предположениями. Во-первых, все небесные тела производят притяжение к их центрам, притягивая не только свои части, как мы это наблюдали на Земле, но и другие небесные тела, находящиеся в сфере их действия. Второе предположение состоит в том, что всякое тело, получившее однажды простое прямолинейное движение, продолжает двигаться по прямой до тех пор, пока не отклонится в своем движении другой действующей силой и не будет вынуждено описывать круг, эллипс или иную сложную линию. Третье предположение заключается в том, что притягивающие силы действуют тем больше, чем ближе тело, на которое они действуют, к центру притяжения».

В 1684 г. английский астроном Эдмунд Галлей показал, что из третьего закона Кеплера должно следовать, что сила тяготения убывает обратно пропорционально квадрату расстояния.

Все, казалось, предугадано, однако сформулировать закон никто не мог, поставленная задача оставалась не решенной. Не хватало понятия массы и математически выраженных законов динамики, которые дали бы возможность решить задачу определения траектории движения тела, на которое действует сила, убывающая обратно пропорционально квадрату расстояния.

Так это представляется нам теперь, когда всматриваемся в глубь истории науки, впервые же эта логическая схема была понята только Ньютоном.

Никто не знал, что законы динамики были сформулированы Ньютоном еще в 1666 г. Невиданная способность выделять в сложности явлений физическую основу и математический гений Ньютона позволили ему решить задачу до конца.

На склоне своих дней Исаак Ньютон рассказал, как произошло открытие им закона всемирного тяготения: он прогуливался рядом с яблоневым садом в имении своих родителей и вдруг увидел Луну в дневном небе. А потом, на его глазах, от ветки оторвалось и упало на землю яблоко.

Поскольку Ньютон в это время как раз работал над законами движения, он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, а значит, на нее влияет какая-то сила, удерживающая от того, чтобы сорваться с орбиты и полететь вдаль, в открытый космос. Здесь ему и пришло в голову, что, возможно, это одна и та же сила заставляет яблоко падать на землю, а Луну оставаться на околоземной орбите.

Закон всемирного тяготения гласит: два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.

где F — модуль вектора силы гравитационного притяжения между телами, обладающих массами и, находящимися на некотором расстоянии друг от друга; G — это коэффициент, который называется гравитационной постоянной.

Гравитационная постоянная, которая фигурирует в современной записи закона всемирного тяготения, отсутствовала в явном виде у Ньютона и в работах других ученых вплоть до начала XIX века. И впервые была введена только после перехода к единой метрической системе мер.

В 1798 году Генри Кавендиш поставил эксперимент с целью определения средней плотности Земли с помощью крутильных весов, изобретённых Джоном Мичелом.

Установка представляла собой деревянное коромысло длиной около 1,8 м с прикреплёнными к его концам небольшими свинцовыми шарами диаметром 5 см и массой 775 г, подвешенное на нити из посеребрённой меди длиной 1 м. К этим шарам с помощью специальной поворотной фермы, ось вращения которой совпадает насколько возможно точно с осью нити, подводились два свинцовых шара большего размера — диаметром 20 см и массой 49,5 кг, жёстко закреплённые на ферме.

Вследствие гравитационного взаимодействия малых шаров с большими коромысло отклонялось на некоторый угол. Зная упругие свойства нити, а также угол поворота коромысла, можно вычислить силу притяжения малого шара к большому, а отсюда и гравитационную постоянную.

Значение гравитационной постоянной, вычисленной Кавендишем, составила

В настоящий момент гравитационная постоянная вычислена с большей точностью и, в современном представлении, она численно равна

Или силе, с которой притягиваются два тела массами 1 кг, находящиеся на расстоянии 1 м друг от друга.

Формула закона всемирного тяготения дает точный результат при расчете силы всемирного тяготения в трех случаях:

1) если размеры тел пренебрежимо малы по сравнению с расстоянием между ними;

2) если оба тела однородны и имеют шарообразную форму;

3) если одно из взаимодействующих тел — шар, размеры и масса которого значительно больше, чем у второго тела (любой формы), находящегося на поверхности этого шара или вблизи нее.

Притяжение тел к Земле — один из случаев всемирного тяготения. Для нас, жителей Земли, эта сила имеет большое значение.

Сила, с которой тело притягивается к Земле, несколько отличается от действующей на это тело силы тяжести. Это связано с тем, что Земля, вследствие ее суточного вращения, не является строго инерциальной системой отсчета. Но поскольку различие между указанными силами существенно меньше каждой из них, эти силы можно считать приблизительно равными.

Значит, для любого тела массой m, находящегося на поверхности Земли или вблизи нее, можно записать, что сила тяжести приблизительно равна силе всемирного тяготения. Из этой формулы можно определить ускорение свободного падения.

Анализируя полученную формулу, видно, что ускорение свободного падения тел, находящихся на поверхности Земли или вблизи нее, зависит от радиуса Земли (т. е. расстояния между центром Земли и данным телом) и ее массы.

Если тело поднять на высоту h над Землей, то расстояние между этим телом и центром Земли будет (R3емли + h). Тогда, в знаменатель нашей формулы необходимо добавить эту высоту. Таким образом, чем больше высота, тем меньше ускорение свободного падения и тем меньше сила тяжести тела. Значит, с увеличением высоты тела над поверхностью Земли действующая на него сила тяжести уменьшается за счет уменьшения ускорения свободного падения.

Но уменьшение это обычно очень невелико, поскольку высота тела над Землей чаще всего пренебрежимо мала по сравнению с радиусом Земли. Например, если альпинист массой 80 кг поднялся на гору высотой 3 км, то действующая на него сила тяжести уменьшится всего на 0,7 Н (или на 0,09%). Поэтому во многих случаях при расчете силы тяжести тела, находящегося на небольшой высоте над Землей, ускорение свободного падения считают равным

пренебрегая его небольшим уменьшением.

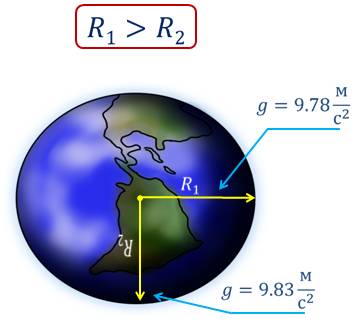
Значения коэффициента g зависит также от географической широты места на земном шаре. Оно меняется от 9,78 м/с2 на экваторе до 9,83 м/с2 на полюсах, т. е. на полюсах оно чуть больше, чем на экваторе. Это и понятно: ведь Земля имеет не строго шарообразную форму. Она немного сплюснута у полюсов, поэтому расстояние от центра Земли до полюсов меньше, чем до экватора.

Подставив в формулу для расчета ускорения свободного падения вместо массы и радиуса Земли соответственно массу и радиус какой-либо другой планеты или ее спутника, можно определить приблизительное значение ускорения свободного падения на поверхности любого из этих небесных тел.

Так ускорение свободного падения на Луне в 6 раз меньше, чем на Земле. Поэтому и сила притяжения тел к Луне в шесть раз меньше, чем на Земле.

Например, человек, масса которого 60 кг, к Земле притягивается с силой 588 Н, а к Луне — с силой 98 Н.

Основные выводы:

– Закон всемирного тяготения гласит: два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.

– Формула закона всемирного тяготения дает точный результат при расчете силы всемирного тяготения в трех случаях:

1) если размеры тел пренебрежимо малы по сравнению с расстоянием между ними;

2) если оба тела однородны и имеют шарообразную форму;

3) если одно из взаимодействующих тел — шар, размеры и масса которого значительно больше, чем у второго тела (любой формы), находящегося на поверхности этого шара или вблизи нее.

– Из закона всемирного тяготения следует, что Земля сообщает любому телу ускорение — ускорение свободного падения, которое зависит от высоты над поверхностью Земли, а так же от географической широты местности.